Cryptographie asymétrique
1. Algorithmes de cryptographie asymétrique
Pour résoudre le problème de l’échange de clés, la cryptographie asymétrique a été mise au point dans les années 1970. Elle se base sur le principe de deux clés :
- une publique, permettant le chiffrement ;
- une privée, permettant le déchiffrement.
Comme son nom l’indique, la clé publique est mise à la disposition de quiconque désire chiffrer un message. Ce dernier ne pourra être déchiffré qu’avec la clé privée, qui doit rester confidentielle.
Ceci dit le rôle des clés est interchangeable : on peut chiffrer avec une clé privées et déchiffrer avec une clé publique.
Quelques algorithmes de cryptographie asymétrique très utilisés :
- RSA (chiffrement et signature);
- DSA (signature);
- Protocole d’échange de clés Diffie-Hellman (échange de clé);
- et d’autres ; voir cette liste plus complète d’algorithmes de cryptographie asymétrique.
Le principal inconvénient de RSA et des autres algorithmes à clés publiques est leur grande lenteur par rapport aux algorithmes à clés secrètes. RSA est par exemple 1000 fois plus lent que DES. En pratique, dans le cadre de la confidentialité, on s’en sert pour chiffrer un nombre aléatoire qui sert ensuite de clé secrète pour un algorithme de chiffrement symétrique. C’est le principe qu’utilisent des logiciels comme PGP par exemple.
La cryptographie asymétrique est également utilisée pour assurer l’authenticité d’un message. L’empreinte du message est chiffrée à l’aide de la clé privée et est jointe au message. Les destinataires déchiffrent ensuite le cryptogramme à l’aide de la clé publique et retrouvent normalement l’empreinte. Cela leur assure que l’émetteur est bien l’auteur du message. On parle alors de signature ou encore de scellement.
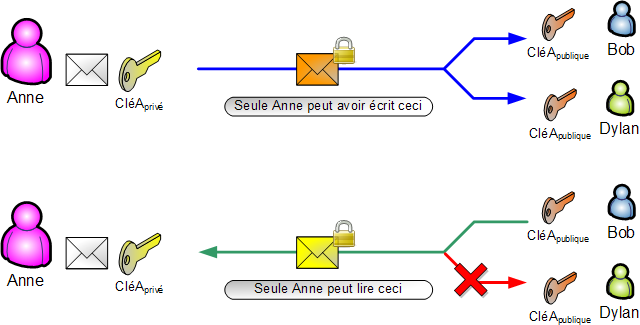
La propriété des algorithmes asymétriques est qu’un message chiffré par une clé publique n’est lisible que par le propriétaire de la clé privée correspondante. À l’inverse, un message chiffré par une clé privée sera lisible par tous ceux qui possèdent la clé publique correspondante.
Ainsi avec sa clé privée, Anne :
- signe ses messages ;
- lit (déchiffre) les messages qui lui sont adressés.
2. Fonctions de hachage
Une fonction de hachage est une fonction qui convertit un grand ensemble en un plus petit ensemble, l’empreinte. Il est impossible de la déchiffrer pour revenir à l’ensemble d’origine, ce n’est donc pas une technique de chiffrement.
Quelques fonctions de hachage très utilisées :
- MD5 ;
- SHA-1 ;
- SHA-256 ;
- et d’autres ; voir cette liste plus complète d’algorithmes de hachage.
L’empreinte d’un message ne dépasse généralement pas 256 bits (maximum 512 bits pour SHA-512) et permet de vérifier son intégrité.
Grâce à la valeur de hachage, on peut discriminer deux objets apparemment proches, ce qui peut être utilisé pour garantir l’intégrité des objets, autrement dit leur non modification par un acteur malveillant.
Le salage (salting en anglais) consiste à ajouter une chaîne de caractères (un nonce) à l’information avant le hachage. Par exemple, dans un cadre cryptographique, au lieu de pratiquer le hachage sur le mot de passe seul, on peut le faire sur le résultat de la concaténation du mot de passe avec une autre chaîne de caractères pseudo-aléatoire, obtenue par un hachage de l’identifiant (login) concaténé avec le mot de passe. Les deux fonctions de hachage (celle qu’on utilise pour générer la chaîne pseudo-aléatoire et celle qu’on applique au résultat) peuvent être différentes (par exemple SHA-1 et MD5).
Cela permet de renforcer la sécurité de cette fonction.
En effet, en l’absence de salage, il est possible de cracker le système à l’aide de tables de hachage correspondant à des valeurs (telles que des mots de passe) souvent utilisées, par exemple les tables arc-en-ciel.
Le simple ajout d’un sel (ou nonce) avant hachage rend l’utilisation de ces tables caduque, et le craquage doit faire appel à des méthodes telles que l’attaque par force brute (cette méthode, consistant à tester toutes les valeurs possibles, prend tellement de temps avec un bon mot de passe que l’on ne peut plus qualifier cela de crackage).
3. Cryptographie hybride
La cryptographie hybride est un système de cryptographie faisant appel aux deux grandes familles de systèmes cryptographiques : la cryptographie asymétrique et la cryptographie symétrique. Les logiciels comme PGP et GnuPG reposent sur ce concept qui permet de combiner les avantages des deux systèmes.
La cryptographie asymétrique propose aussi une autre primitive cryptographique pouvant être associée à un chiffrement symétrique, il s’agit de l’échange de clés (en) ; un exemple est l’échange de clés Diffie-Hellman. Cette méthode, couplée avec un mécanisme d’authentification, est par exemple utilisée par TLS.
La cryptographie asymétrique est intrinsèquement lente à cause des calculs complexes qui y sont associés, alors que la cryptographie symétrique brille par sa rapidité. Toutefois, cette dernière souffre d’une grave lacune, on doit transmettre les clés de manière sécurisée (sur un canal authentifié). Pour pallier ce défaut, on recourt à la cryptographie asymétrique qui travaille avec une paire de clés : la clé privée et la clé publique. La cryptographie hybride combine les deux systèmes afin de bénéficier des avantages (rapidité de la cryptographie symétrique pour le contenu du message) et utilisation de la cryptographie “lente” uniquement pour la clé.
La plupart des systèmes hybrides procèdent de la manière suivante. Une clé aléatoire, appellée clé de session, est générée pour l’algorithme symétrique (3DES, IDEA, AES et bien d’autres encore), cette clé fait généralement entre 128 et 512 bits selon les algorithmes. L’algorithme de chiffrement symétrique est ensuite utilisé pour chiffrer le message. Dans le cas d’un chiffrement par blocs, on doit utiliser un mode d’opération comme CBC, cela permet de chiffrer un message de taille supérieure à celle d’un bloc.
La clé de session quant à elle, se voit chiffrée grâce à la clé publique du destinataire, c’est ici qu’intervient la cryptographie asymétrique (RSA ou ElGamal). Comme la clé est courte, ce chiffrement prend peu de temps. Chiffrer l’ensemble du message avec un algorithme asymétrique serait bien plus coûteux, c’est pourquoi on préfère passer par un algorithme symétrique. Il suffit ensuite d’envoyer le message chiffré avec l’algorithme symétrique et accompagné de la clé chiffrée correspondante. Le destinataire déchiffre la clé symétrique avec sa clé privée et via un déchiffrement symétrique, retrouve le message.
Il est très courant d’ajouter des authentifications et des signatures aux messages envoyés. On utilise pour cela des fonctions de hachage (MD5, SHA-1 ou des codes authentificateurs comme HMAC).

4. Exercices de cryptographie asymétrique
4.1. Générer l’emprunte d’un fichier
echo "fichier" > fichier.txt
echo "cichier" > fichier2.txt
openssl dgst -md5 < fichier.txt
(stdin)= f177a99d010fa7406403cd2136e7644e
openssl dgst -md5 < fichier2.txt
(stdin)= ced7ffe67001ba15b5a4ef4d0d20269a
openssl dgst -sha1 < fichier.txt
(stdin)= 47629f27e6f98a000d9a51907fa706e676d6eee8
openssl dgst -sha1 < fichier2.txt
(stdin)= 828968c2043569a701bfaf2e8cf94a612e3ec410
openssl dgst -sha256 < fichier.txt
(stdin)= 07ae4c332cc992ea1086d067b0e720a914e601c9d3b016f9952cd8a05e03cdfc
openssl dgst -sha256 < fichier2.txt
(stdin)= ceb3564c37c7775d5d5611724de0f566dc7d6f5797f1e16da9ccdb3efa7f7b84
openssl dgst -sha512 < fichier.txt
(stdin)= 69f0cc9551f59aee2496c9ff4f492325c9cb1379a6a83c36ddd1e5e3f751344da52435306f9c1cf00cc68ba4e97fa2e84123e01f50b0227dfbb6cc63e1530c95
openssl dgst -sha512 < fichier2.txt
(stdin)= 778c653c8381416901e9fd0ab2fa01b6c65171594906ab48c60d81cdf8596cd3091f391213ed834e187fdee6c4d0f96100d7672ea5f5db65ab23abef020b919d
Aussi on peut utiliser les binaires md5sum, sha1sum, sha224sum, sha256sum, sha384sum, sha512sum.
Par exemple :
sha1sum fichier.txt
47629f27e6f98a000d9a51907fa706e676d6eee8 fichier.txt
sha1sum fichier.txt > fichier.txt.sha1
sha1sum -c fichier.txt.sha1
fichier.txt: Réussi
4.2. Exercices de chiffrement asymétrique
Alice génère un couple de clés :
openssl genrsa -out cle.pem 2048
Generating RSA private key, 2048 bit long modulus
...........................................+++
...................+++
e is 65537 (0x10001)
Alice extrait sa clé publique et la transmet à Bob :
openssl rsa -in cle.pem -pubout -out pub.pem
writing RSA key
Bob envoie un mot de passe chiffré avec la clé publique d’Alice :
echo secret | openssl rsautl -inkey pub.pem -pubin -out crypto.dat -encrypt
cat crypto.dat
��=�|˂ʔ1���EU�u5����~�s
���"4��Nf
�Z_�&fmp}UÏ��+��[��G��\��!m�4�;!����q����>��2�`D�EV��@��y��2�A���+9��M�KG#��^��<d�@�C"�!v�t�*|��^�8�z�$��`R�;.�;� X����jD1��!�׀\�`��Z?89
ּ
z,Z*�
Alice déchiffre le mot de passe :
openssl rsautl -inkey cle.pem -in crypto.dat -decrypt
secret

4.3. Exercice de signature numérique
Alice calcule l’empreinte d’un fichier en sha1 et la signe avec la clé privée avec openssl :
echo "test" > fic_a_signer.txt
openssl dgst -sha1 fic_a_signer.txt > sign.sha1
openssl rsautl -sign -in sign.sha1 -inkey cle.pem -out clair.sig
Bob reçoit le fichier et la signature, il recalcule l’emprunte et il déchiffre la signature avec la clé publique d’Alice. Si les deux valeurs sont identiques le message est bien signé.
$ openssl dgst -sha1 fic_a_signer.txt
SHA1(fic_a_signer.txt)= 4e1243bd22c66e76c2ba9eddc1f91394e57f9f83
openssl rsautl -verify -in clair.sig -inkey pub.pem -pubin
SHA1(fic_a_signer.txt)= 4e1243bd22c66e76c2ba9eddc1f91394e57f9f83
